Teorija Matematika - Test 4
Deo matematike koji proučava izvode zove se:
Diferencijalni račun
Integralni račun
Diskretni račun
Matrični račun
Tvorci diferencijalnog računa su:
Njutn I Laplas
Njutn I Lagranž
Njutn I Lajbnic
Njutn I Lopital
Problem tangente prvi je rešio:
Njutn
Lagranž
Lajbnic
Lopital
Izvod funkcije po definiciji iznosi:
0%
0
0%
0
0%
0
0%
0
Levi izvod funkcije po definiciji iznosi:
0%
0
0%
0
0%
0
0%
0
Desni izvod funkcije po definiciji iznosi:
0%
0
0%
0
0%
0
0%
0
Ako je funkcija diferencijabilna u tački ona:
Ima izvod u toj tački
Nema izvod u toj tački
Neprekidna je u toj tački
Nije neprekidna je u toj tački
Funkcija je diferencijabilna u tački ako je:
Postoje levi izvod I desni izvod, I jednaki su
Postoje levi izvod I desni izvod, I nisu jednaki
Levi izvod jednak desnom izvodu, I moraju da budu jednaki vrednosti funkcije u toj tački
Dovoljno je da postoji samo jedan od izvoda (levi ili desni)
Pravila diferenciranja su:
( Cf (x))' = C' f'(x)
( Cf (x))' = C'
( Cf (x))' = f' (x)
( Cf (x))' = C f'(x)
Pravila diferenciranja su:
0%
0
0%
0
0%
0
0%
0
Pravila diferenciranja su:
0%
0
0%
0
0%
0
0%
0
Pravila diferenciranja su:
0%
0
0%
0
0%
0
0%
0
Geometrijsko tumačenje izvoda:
Vrednost prvog izvoda u dodirnoj tački jednak je koeficijentu pravca tangente u toj tački
Vrednost drugog izvoda u dodirnoj tački jednak je koeficijentu pravca tangente u toj tački
Vrednost prvog izvoda u dodirnoj tački jednak je koeficijentu pravca tangente u bilo kojoj tački
Vrednost prvog izvoda u dodirnoj tački jednak je koeficijentu pravca normale na tangentu u toj tački
Izvod složene funkcije se izračunava po formuli:
0%
0
0%
0
0%
0
0%
0

0%
0
0%
0
0%
0
0%
0
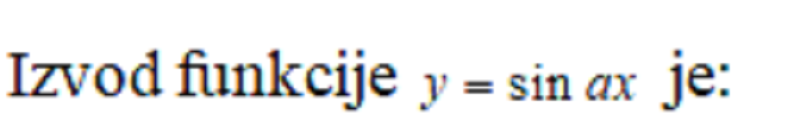
0%
0
0%
0
0%
0
0%
0
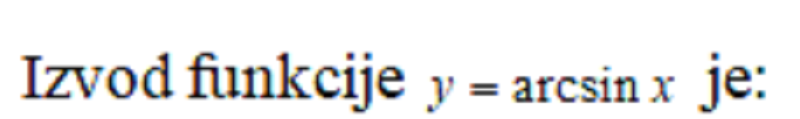
0%
0
0%
0
0%
0
0%
0
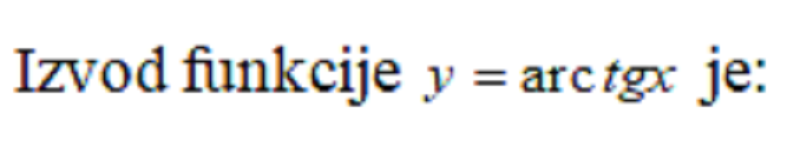
0%
0
0%
0
0%
0
0%
0
Lopitalova teorema omogućava:
Izračunavanje limesa nekih neodređenih izraza
Izračunavanje limesa svih izraza
Zadate funkcije moraju da budu diferencijabilne
Zadate funkcije ne moraju da budu diferencijabilne
Lopitalova teorema važi za:
0%
0
0%
0
0%
0
0%
0
Lopitalova teorema koristi se za neodređenosti:
0 / 0
0 / beskonacno
Beskonacno / beskonacno
Beskonacno / 0
Lopitalova teorema koristi se I za neodređenosti:
0%
0
0%
0
0%
0
0%
0
Lopitalova teorema za diferencijabilne funkcije f I g glasi:
0%
0
0%
0
0%
0
0%
0
Stacionarna tačka je ona tačka:
U kojoj funkcija mora da ima ekstrem
U kojoj funkcija može da ima ekstrem
Potreban, ali ne I dovoljan uslov za ekstrem
To je nula prvog izvoda
Ako je f' (x) > 0 onda je funkcija u tom intervalu:
Rastuća
Opadajuća
Konveksna
Konkavna
Ako je f' (x) < 0 onda je funkcija u tom intervalu:
Rastuća
Opadajuća
Konveksna
Konkavna
Ako je f'' (x) > 0 onda je funkcija u tom intervalu:
Rastuća
Opadajuća
Konveksna
Konkavna
Ako je f'' (x) < 0 onda je funkcija u tom intervalu:
Rastuća
Opadajuća
Konveksna
Konkavna
Kod monotono rastuće funkcije na nekom intervalu je:
0%
0
0%
0
0%
0
0%
0
Kod monotono ne rastuće funkcije na nekom intervalu je:
0%
0
0%
0
0%
0
0%
0
Kod monotono opadajuće funkcije na nekom intervalu je:
0%
0
0%
0
0%
0
0%
0
Kod monotono neopadajuće funkcije na nekom intervalu je:
0%
0
0%
0
0%
0
0%
0
Ekstrem funkcije je tačka:
U kojoj je prvi izvod nula
Nula prvog izvoda je potreban uslov za ekstrem
Tačka u kojoj dolazi do promene monotonosti
Tačka u kojoj dolazi do promene konveksnosti
Ekstremi su:
Tačke u kojima funkcija izvoda menja znak
Tačke u kojima funkcija menja smisao monotonosti
Najveća I najmanja vrednost funkcije
Min I max
Maksimum funkcije je:
0%
0
0%
0
0%
0
0%
0
Minimum funkcije je:
0%
0
0%
0
0%
0
0%
0
Prevojna tačka je:
Nula prvog izvoda
Nula drugog izvoda
Tačka u kojoj funkcija iz opadanja prelazi u rašćenje
Tačka u kojoj funkcija iz konveksnosti prelazi u konkavnost
Funkcija je konveksna:
0%
0
0%
0
0%
0
0%
0
Funkcija je konkavna:
0%
0
0%
0
0%
0
0%
0
Dovoljan uslov za ekstrem u tački x je:
Da izvodna funkcija menja znak pri prolazu kroz tačku x
Da izvodna funkcija ne menja znak pri prolazu kroz tačku x
Da je f' (x) = 0
Da je f'' (x) = 0
Potreban uslov za ekstrem u tački x je:
Da izvodna funkcija menja znak pri prolazu kroz tačku x
Da izvodna funkcija ne menja znak pri prolazu kroz tačku x
Da je f' (x) = 0
Da je f'' (x) = 0
Lokalni maksimum je:
Najveća vrednost funkcije na intervalu
Ekstrem
Tačka u kojoj mora da je f' (x) = 0
Tačka u kojoj može da je f' (x) = 0
151. Lokalni minimum je:
Najveća vrednost funkcije na intervalu
Ekstrem
Tačka u kojoj mora da je f' (x) = 0
Tačka u kojoj može da je f' (x) = 0
(Poslednje pitanje) Mehaničko tumačenje izvoda:
Trenutna brzina
Srednja brzina
Trenutno ubrzanje
Srednje ubrzanje
{"name":"Teorija Matematika - Test 4", "url":"https://www.quiz-maker.com/QPREVIEW","txt":"Deo matematike koji proučava izvode zove se:, Tvorci diferencijalnog računa su:, Problem tangente prvi je rešio:","img":"https://www.quiz-maker.com/3012/CDN/98-4831808/image-2024-02-14-061844487.png?sz=1200"}
